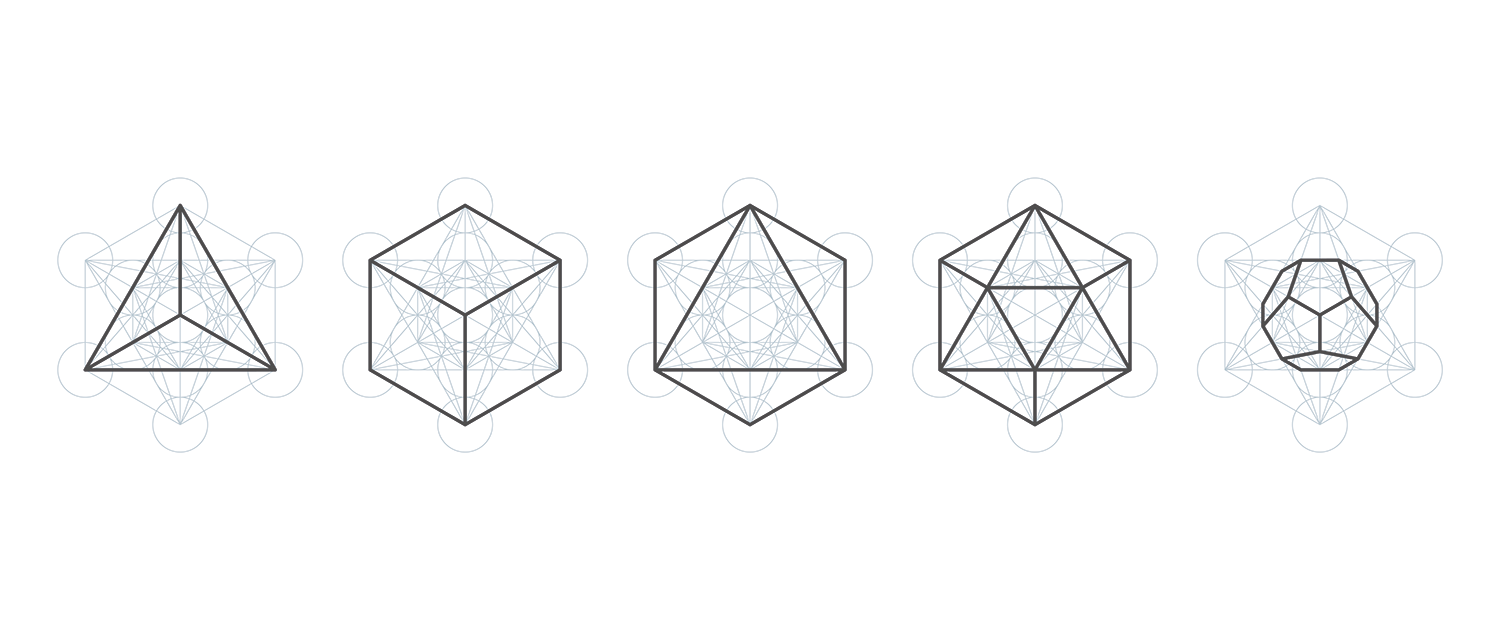
Diese mystischen Formen - Tetraeder, Hexaeder, Oktaeder, Dodekaeder und Ikosaeder - haben nicht nur in der Mathematik und Geometrie, sondern auch in kunstvollen Architektur- und Designs einen Einfluss. Ihre erstaunliche Symmetrie und Ästhetik haben viele Künstler und Designer inspiriert.

In diesem Artikel nehmen wir Sie mit auf eine aufregende Reise, bei der Sie die Grundlagen der platonischen Körper entdecken werden. Von ihren einzigartigen Eigenschaften bis hin zu ihren Anwendungen in verschiedenen Bereichen werden wir die faszinierende Welt der platonischen Körper enthüllen. Machen Sie sich bereit, in die faszinierende Welt der Mathematik einzutauchen!

Einführung in die platonischen Körper

Die platonischen Körper sind eine der faszinierendsten Entdeckungen in der Geometrie. Diese speziellen dreidimensionalen Formen zeichnen sich durch ihre perfekten symmetrischen Eigenschaften aus. Sie bestehen aus polygonalen Flächen, die gleichmäßig und regelmäßig angeordnet sind. Jedes dieser Formen hat die gleiche Anzahl von Gesichtern, Kanten und Ecken, was ihnen eine bemerkenswerte Harmonie verleiht. In der Mathematik sind platonische Körper nicht nur geometrische Objekte, sondern auch Schlüssel zur Untersuchung von Symmetrie und Raum.

Die fünf platonischen Körper sind der Tetraeder, das Hexaeder, das Oktaeder, der Dodekaeder und das Ikosaeder. Jeder dieser Körper ist einzigartig in seiner Struktur und seinen Eigenschaften, und sie alle haben eine lange Geschichte, die bis in die Antike zurückreicht. Sie wurden von Philosophen und Mathematikern studiert, die ihre tiefere Bedeutung in der Natur und in der Kunst suchten. Die platonischen Körper sind nicht nur theoretische Konstrukte; sie finden auch in der realen Welt Anwendung, sei es in der Architektur, in der Kunst oder in der Naturwissenschaft.

In dieser Einführung werden wir die grundlegenden Konzepte und die Bedeutung der platonischen Körper näher betrachten. Wir werden untersuchen, warum diese geometrischen Formen so entscheidend für das Verständnis von Raum und Symmetrie sind und welche Rolle sie in verschiedenen wissenschaftlichen Disziplinen spielen. Die Reise in die Welt der platonischen Körper ist nicht nur eine mathematische Erkundung, sondern auch eine Entdeckung der Ästhetik und der Schönheit der Geometrie.

Die fünf platonische Körper in der Übersicht. Von links nach rechts: Tetraeder, Hexaeder, Oktaeder, Dodekaeder und Ikosaeder

Geschichte der platonischen Körper

Die Entdeckung der platonischen Körper reicht bis in die Antike zurück, als der griechische Philosoph Platon sie in seinen Dialogen erwähnte. Platon verband die platonischen Körper mit den Elementen der Natur – Erde, Wasser, Luft und Feuer – und sah in ihnen die Grundbausteine des Universums. Seine Schüler und Nachfolger, insbesondere der Mathematiker Euklid, trugen zur systematischen Untersuchung dieser Formen bei, indem sie sie in seinen Werken wie den „Elementen“ dokumentierten.

Im Laufe der Jahrhunderte wurden die platonischen Körper von verschiedenen Kulturen und Wissenschaftlern erforscht. Im Mittelalter wurden sie von Mathematikern wie Johannes Kepler weiter untersucht, der versuchte, ihre Beziehung zu den Planeten und dem Sonnensystem zu verstehen. Kepler postulierte sogar, dass die platonischen Körper als „Raumgefüge“ der Planeten dienen könnten, was das Interesse an diesen geometrischen Formen weiter steigerte.

Die Wiederentdeckung der platonischen Körper während der Renaissance führte zu einem neuen Verständnis ihrer ästhetischen und mathematischen Bedeutung. Künstler wie Leonardo da Vinci und Albrecht Dürer schufen Werke, die von den perfekten Formen und Symmetrien der platonischen Körper inspiriert wurden. Diese Zeit markierte einen Wendepunkt in der Verbindung zwischen Kunst und Mathematik, die bis heute anhält. Die platonischen Körper wurden nicht nur als mathematische Objekte betrachtet, sondern auch als Symbole für Harmonie und Schönheit in der Welt.

Eigenschaften der platonischen Körper

Die platonischen Körper besitzen einige bemerkenswerte Eigenschaften, die sie von anderen geometrischen Formen unterscheiden. Zunächst sind sie konvex, was bedeutet, dass alle ihre inneren Winkel kleiner als 180 Grad sind und sie keine Vertiefungen oder Löcher aufweisen. Diese Eigenschaft macht sie besonders stabil und gleichmäßig. Darüber hinaus ist jeder platonische Körper durch seine regelmäßigen polygonalen Flächen definiert, die alle gleich sind. Diese Regelmäßigkeit verleiht ihnen eine harmonische Symmetrie, die in der Natur und der Architektur häufig vorkommt.

Ein weiteres bemerkenswertes Merkmal der platonischen Körper ist ihre Symmetrie. Jeder Körper hat eine bestimmte Anzahl von Symmetrieachsen, und die Anzahl dieser Achsen ist direkt mit der Anzahl der Gesichter, Kanten und Ecken verbunden. Diese Symmetrie ist nicht nur ästhetisch ansprechend, sondern spielt auch eine wichtige Rolle in der Physik und Chemie. Beispielsweise sind viele Moleküle und Kristalle nach platonischen Körpern strukturiert, was ihre Stabilität und Reaktivität beeinflusst.

Zusätzlich zu ihrer geometrischen Schönheit haben platonische Körper auch interessante mathematische Eigenschaften. Sie sind die einzigen konvexen Polyeder, die aus gleichmäßigen polygonalen Flächen bestehen. Diese Tatsache führt zu wichtigen mathematischen Beziehungen und Formeln, die in der Geometrie von Bedeutung sind. Die platonischen Körper sind daher nicht nur ein ästhetisches Phänomen, sondern auch ein tiefes mathematisches Konzept, das in vielen Bereichen der Wissenschaft Anwendung findet.

Mathematische Formeln und Berechnungen

Die platonischen Körper sind nicht nur faszinierende geometrische Formen, sondern auch Gegenstand zahlreicher mathematischer Berechnungen. Jede dieser Formen hat spezifische Eigenschaften, die durch mathematische Formeln ausgedrückt werden können. Zu den wichtigsten Größen, die für platonische Körper berechnet werden, gehören Volumen, Fläche und die Beziehung zwischen den Kanten, Gesichtern und Ecken.

Das Volumen eines platonischen Körpers kann mithilfe spezieller Formeln berechnet werden. Für den Tetraeder beträgt das Volumen V = (a³ / 6√2), wobei a die Kantenlänge ist. Für das Hexaeder, auch als Würfel bekannt, lautet die Formel V = a³. Das Volumen des Oktaeders kann mit der Formel V = (a³ / 3√2) berechnet werden, während der Dodekaeder und das Ikosaeder komplexere Formeln erfordern, die auf ihren einzigartigen Strukturen basieren.

Die Flächenberechnung ist ebenso wichtig. Für den Tetraeder beträgt die Oberfläche A = √3a², während der Würfel eine Fläche von A = 6a² hat. Das Oktaeder hat eine Fläche von A = 2√3a², der Dodekaeder A = 3√25 + 10√5 a² und das Ikosaeder A = 5√3a². Diese Formeln sind nicht nur für die theoretische Mathematik von Bedeutung, sondern finden auch in praktischen Anwendungen, wie der Architektur und der Materialwissenschaft, Verwendung.

Ein weiterer interessanter Aspekt der platonischen Körper ist ihre Beziehung zwischen Ecken (V), Kanten (K) und Flächen (F), die durch die Euler'sche Formel beschrieben wird: V - K + F = 2. Diese Formel gilt für alle konvexen Polyeder und ist ein grundlegendes Konzept in der Topologie. Die platonischen Körper bieten daher nicht nur eine ästhetische Anziehungskraft, sondern auch eine mathematische Tiefe, die für Mathematiker und Wissenschaftler von großem Interesse ist.

Bedeutung der platonischen Körper in der Geometrie

Die platonischen Körper spielen eine zentrale Rolle in der Geometrie, da sie die Basis für viele geometrische Konzepte und Theorien bilden. Sie sind die einzigen konvexen Polyeder, die ausschließlich aus regelmäßigen Polygonen bestehen, was sie zu einem einzigartigen Studienobjekt macht. Ihr Einfluss erstreckt sich über verschiedene Bereiche der Mathematik, von der reinen Geometrie bis hin zur algebraischen Topologie.

In der Geometrie werden platonische Körper als Modelle verwendet, um komplexe Konzepte wie Symmetrie, Raum und Dimension zu veranschaulichen. Sie helfen dabei, das Verständnis von dreidimensionalem Raum zu fördern und bieten eine klare und strukturierte Möglichkeit, geometrische Beziehungen zu analysieren. Darüber hinaus sind sie von grundlegender Bedeutung für das Studium von Polyedern, da sie die einfachsten und regelmäßigsten Formen darstellen.

Die platonischen Körper sind auch eng mit den Konzepten der Gruppentheorie verbunden, da ihre Symmetrien durch mathematische Gruppen beschrieben werden können. Diese Symmetrien sind nicht nur von theoretischem Interesse, sondern finden auch praktische Anwendungen in Bereichen wie der Physik und der Chemie, wo sie dabei helfen, die Struktur von Molekülen und Kristallen zu verstehen. Insgesamt sind die platonischen Körper ein unverzichtbares Element der geometrischen Theorie und Praxis.

Symmetrie und Ästhetik der platonischen Körper

Die Symmetrie der platonischen Körper ist eines ihrer herausragendsten Merkmale und trägt wesentlich zu ihrer Ästhetik bei. Jeder platonische Körper hat eine hohe Symmetrie, die sich in der gleichmäßigen Anordnung seiner Flächen, Kanten und Ecken widerspiegelt. Diese Symmetrie ist nicht nur mathematisch von Bedeutung, sondern hat auch eine tiefere ästhetische Dimension, die Künstler und Designer inspiriert hat, seit die platonischen Körper erstmals entdeckt wurden.

Die verschiedenen Arten der Symmetrie, die in den platonischen Körpern vorkommen, umfassen Rotationssymmetrie und Spiegelungssymmetrie. Rotationssymmetrie bedeutet, dass der Körper um eine Achse gedreht werden kann, ohne dass sich sein Erscheinungsbild verändert. Spiegelungssymmetrie bezieht sich auf die Fähigkeit, den Körper entlang einer Achse zu spiegeln, sodass die beiden Hälften identisch sind. Diese Symmetrien verleihen den platonischen Körpern nicht nur ihre mathematische Schönheit, sondern auch eine gewisse Harmonie und Ausgewogenheit, die in der Natur häufig vorkommt.

Die Ästhetik der platonischen Körper hat Künstler und Architekten über Jahrhunderte hinweg fasziniert. Viele Werke der Kunst und Architektur sind direkt von den Formen und Symmetrien der platonischen Körper inspiriert. Sie finden sich in der Architektur von Tempeln, Monumenten und modernen Gebäuden ebenso wie in der bildenden Kunst. Diese ästhetische Anziehungskraft der platonischen Körper zeigt, wie eng Mathematik, Kunst und Natur miteinander verbunden sind. Die Erforschung dieser Beziehungen eröffnet neue Perspektiven für das Verständnis der Welt um uns herum.

Anwendungen der platonischen Körper in der Natur und Architektur

Die platonischen Körper finden sich nicht nur in der reinen Mathematik, sondern auch in vielen Bereichen der Natur und Architektur. In der Natur erscheinen sie häufig in Kristallen und Molekülen. Die Struktur von DNA, das als Ikosaeder modelliert werden kann, ist ein Beispiel dafür, wie die platonischen Körper in biologischen Systemen integriert sind. Auch die Geometrie von Schneeflocken und anderen natürlichen Formen zeigt oft platonische Eigenschaften, was die tiefere Verbindung zwischen Mathematik und Natur verdeutlicht.

In der Architektur wurden platonische Körper als Prinzipien für die Gestaltung von Gebäuden und Strukturen verwendet. Viele berühmte Bauwerke, wie das Guggenheim-Museum in Bilbao oder das Eden Project in Großbritannien, nutzen die geometrischen Eigenschaften der platonischen Körper, um ästhetisch ansprechende und funktionale Räume zu schaffen. Diese Körper bieten nicht nur strukturelle Integrität, sondern auch eine visuelle Anziehungskraft, die Menschen in ihren Bann zieht.

Die Anwendung platonischer Körper in der Technologie ist ebenfalls bemerkenswert. In der Computergraphik werden sie häufig verwendet, um komplexe dreidimensionale Modelle zu erstellen. Sie dienen als Grundlage für die Erstellung von 3D-Objekten in Videospielen, Animationen und Simulationen. Diese praktischen Anwendungen verdeutlichen, wie die theoretischen Konzepte der platonischen Körper in der modernen Welt von Bedeutung sind und wie sie in verschiedenen Disziplinen integriert werden können.

Die fünf platonischen Körper im Detail: Tetraeder, Hexaeder, Oktaeder, Dodekaeder, Icosaeder

Die platonischen Körper bestehen aus fünf einzigartigen Formen, die sich durch ihre geometrischen Eigenschaften unterscheiden. Der Tetraeder ist der einfachste der platonischen Körper und besteht aus vier gleichseitigen Dreiecken. Er hat vier Ecken, sechs Kanten und vier Flächen. Der Tetraeder ist besonders bemerkenswert, weil er das einzige platonische Körper ist, das aus nur einem Typ von Fläche besteht und somit eine hohe Symmetrie aufweist.

Das Hexaeder, auch bekannt als Würfel, ist der bekannteste platonische Körper. Es besteht aus sechs quadratischen Flächen, hat acht Ecken und zwölf Kanten. Die Form des Würfels ist in der Natur und in der Architektur weit verbreitet. Seine regelmäßige Struktur und einfache Symmetrie machen ihn zu einem beliebten Element in Design und Kunst.

Das Oktaeder ist ein weiterer faszinierender platonischer Körper, der aus acht gleichseitigen Dreiecken besteht. Es hat sechs Ecken und zwölf Kanten. Das Oktaeder hat eine interessante Eigenschaft: Wenn man zwei Tetraeder zusammenfügt, erhält man ein Oktaeder. Diese Beziehung zeigt, wie die platonischen Körper miteinander verbunden sind und wie sie sich gegenseitig ergänzen können. Der Dodekaeder, mit seinen zwölf regelmäßigen Fünfecken, und das Ikosaeder, das aus zwanzig gleichseitigen Dreiecken besteht, runden die Gruppe der platonischen Körper ab. Beide haben komplexe Strukturen und faszinierende Eigenschaften, die sie zu einem wichtigen Bestandteil der Mathematik und Geometrie machen.

Entdecken Sie die Schönheit der platonischen Körper in der Kunst

Die platonischen Körper haben Künstler und Designer über die Jahrhunderte hinweg inspiriert. Ihre harmonischen Formen und Symmetrien sind nicht nur mathematische Konzepte, sondern auch Quellen künstlerischer Kreativität. In der Malerei, Bildhauerei und Architektur finden sich zahlreiche Beispiele für die Verwendung platonischer Körper, die die Verbindung zwischen Kunst und Mathematik verdeutlichen.

Ein bekanntes Beispiel ist die Arbeit des Künstlers M.C. Escher, der oft mit geometrischen Mustern und den platonischen Körpern experimentierte. Seine Werke zeigen, wie komplexe geometrische Beziehungen in ästhetisch ansprechende Kompositionen umgesetzt werden können. Eschers Verwendung von Symmetrie und unendlichen Mustern ist ein Beweis für die tiefen Verbindungen zwischen Mathematik und Kunst.

Darüber hinaus finden sich platonische Körper in der modernen Architektur, wo sie als Inspiration für innovative Designs dienen. Architekten nutzen diese Formen, um Räume zu schaffen, die sowohl funktional als auch visuell ansprechend sind. Die Verwendung platonischer Körper in der Architektur zeigt, wie mathematische Prinzipien und ästhetische Überlegungen miteinander verschmelzen können, um beeindruckende Bauwerke zu schaffen.

In der zeitgenössischen Kunst und Skulptur sind platonische Körper ebenfalls ein beliebtes Motiv. Künstler verwenden sie, um Konzepte wie Raum, Struktur und Bewegung zu erforschen. Die platonischen Körper bieten eine visuelle und konzeptionelle Grundlage, die es Künstlern ermöglicht, mit Form und Raum zu experimentieren und neue Wege der Darstellung zu finden.

Zusammenfassung

Die platonischen Körper sind ein faszinierendes Studienobjekt, das die Grenzen zwischen Mathematik, Kunst und Natur überwindet. Ihre einzigartigen Eigenschaften und Symmetrien machen sie zu einem wichtigen Thema in der Geometrie und bieten gleichzeitig eine Quelle der Inspiration für Künstler und Designer. Von ihren historischen Wurzeln in der Antike bis hin zu ihren modernen Anwendungen in Wissenschaft und Kunst haben platonische Körper die Menschheit über Jahrhunderte hinweg begeistert.

In diesem Artikel haben wir die verschiedenen Aspekte der platonischen Körper betrachtet, einschließlich ihrer Geschichte, Eigenschaften, mathematischen Formeln und Anwendungen. Die bedeutende Rolle, die sie in der Geometrie spielen, sowie ihre ästhetische Anziehungskraft zeigen, wie eng Mathematik mit der Welt um uns herum verbunden ist. Die platonischen Körper sind nicht nur geometrische Objekte, sondern auch Symbole für Harmonie, Schönheit und Struktur in der Natur.

Abschließend lässt sich sagen, dass die platonischen Körper nicht nur ein Thema für Mathematiker sind, sondern auch eine Quelle der Inspiration für Künstler, Architekten und Wissenschaftler. Ihre zeitlose Anziehungskraft und ihre tiefere Bedeutung werden auch in Zukunft weiterhin das Interesse und die Neugier der Menschen wecken. Die Reise in die faszinierende Welt der platonischen Körper ist ein eindrucksvolles Beispiel dafür, wie Mathematik und Kunst auf harmonische Weise miteinander verbunden sind.